The maths behind 'The Years Between'
I thought I'd do a little look into the Interval mechanics in Twilight Song, since I used computer simulations of the game to design this part, and as far as I know, that's not something many people do. This is the only part of the game that's mechanically complex, too—much like The Quiet Year, the game Twilight Song is extensively hacked from, the rules are for the most part pretty plain, simple, and easily-understood.
Intervals: 'Story Years' vs 'Years Between'
Like The Quiet Year (TQY), Twilight Song (TS) uses a season oracle and deck of cards to create random events; unlike TQY, a game of TS can span many in-game years. In TQY you draw all the Spring cards, then all Summer, etc.; in TS you can draw from the current season or the next one. Then:
- When you reach the end of the year, you play an Interval turn and loop back round to Spring.
- When a season runs out of cards, it just... doesn't happen any more. TS is about endings as much as changes and beginnings.
- When you run out of cards, the game ends.
Between each 'story year' there's an Interval turn, 'the years between'. The interval could be 1 night, a few years, about a decade, or a whole generation. Intervals have their own rules and oracle—you can see some of the mechanics in the freely-downloadable Interval Oracle attached to this devlog and on the game's main page.
The reason for special Interval mechanics, rather than just letting players decide how much time passes as a group, is to add some unpredictability to the game and to put more focus on regular events rather than sculpted overarching stories.
Designing the Mechanic
Way back in the alpha playtest version this was very simple. We played on roll20 and I added a separate 13-card Interval deck. During Winter, a player could draw from Winter or from the Interval deck; if they picked Interval, the player after them had to draw from Spring. Each card had the number of years that passed and a narrative prompt like a regular season card:

The problem is, a regular deck of cards only has 4 suits and this needs 5. I wanted TS to be simpler and easier to prep for, so I went back to the drawing board and came up with 2 new ideas. Both used the cards you'd already drawn in the previous year, so there's no need for extra cards or suits:
- Low Card: At the end of the year, check the most recent cards drawn for each season in that year. Find the lowest card (jack = 11, queen = 12, king = 13):
- Ace, 1 night passes;
- 2-3, a few years pass;
- 4-6, a decade passes;
- 7+, a generation passes.
- High Season: look at the most recent cards drawn last year for each season. Find the season with the highest card (if there's a tie, earlier season wins):
- Spring, 1 night passes;
- Summer, a few years pass;
- Autumn, a decade passes;
- Winter, a generation passes.
If the last cards you drew in each season last year were: Spring 4, Summer K, Autumn 7, Winter 8: Low Card is 4, which would mean a decade passes (since 4 falls in 4-6). High Season is Summer, which would mean a few years pass.
So far so good. Low Card is more complex, but I can fine-tune it by tweaking the ranges. High Season is simpler, but stiffer. They each have advantages and disadvantages... so it's hard to pick.
Introducing: Maths
Now, I could playtest loads with each mechanic, but this isn't an abstract, game-feel-y issue—I know what I want in numerical terms:
- longer intervals to always be less likely than shorter ones (how likely is each interval type overall?);
- every interval to be very likely to happen at least once per game (how likely is it that an interval will happen at least once per game?);
- a game to span about 50-100 years, on average (how long do games run for (in-game years)?).
These are all numerical, statistical questions, and there's only 1 factor under player control: how likely people are to stay in the same season as last turn when they draw a card. I can just set that to different levels to get different data, and look at all the data together. Anyway, I wrote some code to basically play the card-drawing part of the game. In fact, it played 10000 games at a time—the more games, the more accurate the results (with diminishing returns).
What's a simulation?
(You can read this if you're curious, or skip ahead to the results in the next sections.)
A simulation is a model or representation of something changing over time. Key parts #1: model/representation, it's simplified but close enough to reality. Hard mechanics are easy to simulate. Player choice is harder, so it tends to get simplified way more. Key part #2: changing over time, so what happens earlier affects what happens later.
Let's say you roll a d6 one hundred times and write down every result. You've get, on average, 16-17 ones, 16-17 twos, and so on. None of the earlier results affect the later ones, though. There's no point simulating this over time. Now let's say you shuffle a deck of cards and draw the top card—it's a 7 of Hearts. You set it aside. The probability of getting each card—including the 7 of Hearts—has now changed in the next draw. There is a reason to simulate this over time, because what happens earlier affects what happens later.
That's not to say dice mechanics are never worth simulating and card mechanics are always worth simulating. You can come up with more complicated dice mechanics where the system does change over time, and you could, if you really, really wanted, reshuffle the deck after every draw. That said, it shows the difference between dice and cards: it's quick to reset dice (pick them up and roll them again) and slow to reset cards (collect them all and reshuffle the deck).
I coded my simulation in MATLAB, which is a proprietary programming environment that handles data fairly well. If you have at least a little programming experience it's not hard to simulate this stuff yourself—if you don't, don't worry, I'm not gonna go into the details. The simulation does more-or-less the same things the players would do, just in code rather than flesh and cardstock. The only player choice is whether to draw from the same season or the next one, which I simplified to a single probability (like the computer rolling a die or flipping a coin). Is this realistic? Nah. Some people will decide on the spur of the moment, but others will judge it based on how the story's going, whether they want to advance time, etc. The probability just sums up all effects of all these thought processes without having to model incredibly complex things like 'story' and 'want'.
A good simulation shows you reasonable possibilities, not absolute truths.
Q1: how likely is each interval type overall?
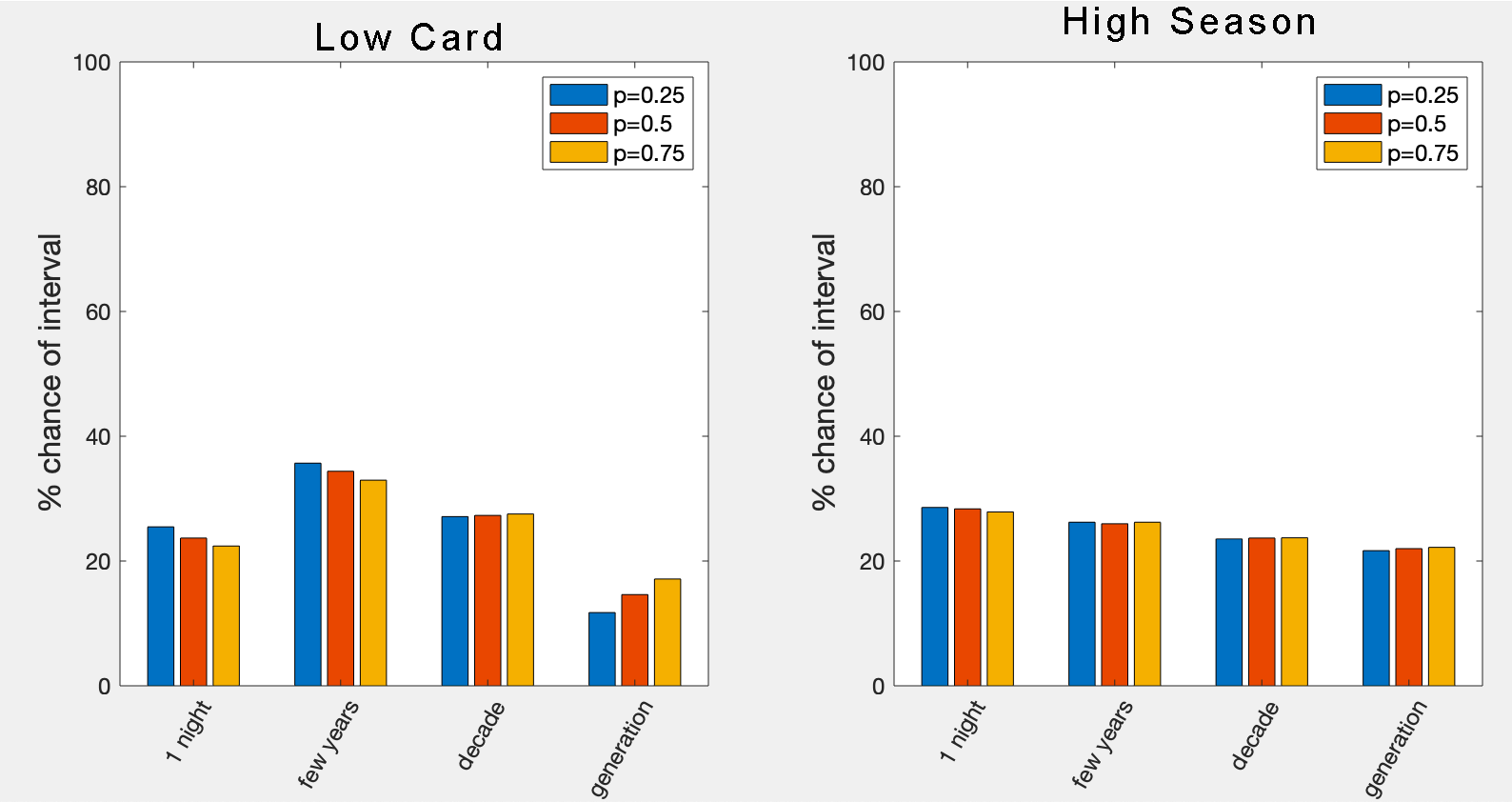
Why am I interested in this? I want the game to skew towards shorter intervals so that you get a cluster of story years together, then a longer interval, then another cluster, and so on.
What are the results? Bar charts of the percent chance that an Interval will be each length. p=0.25 means there's a 25% chance a player stays in the same season when drawing a card. I'm most interested in p=0.5 in these results and the ones below (i.e. people are as likely to stay in one season as go to the next), since that was my experience in playtesting.
What does this show? High Season is more what I want: longer intervals are always less likely than shorter ones and there aren't any emergent surprises (e.g. in Low Card where 'a generation' gets more likely the more cards you draw). I'd like it if shorter intervals were a little more likely and longer ones were less likely, but ah well.
Q2: how likely is it that an interval will happen at least once per game?
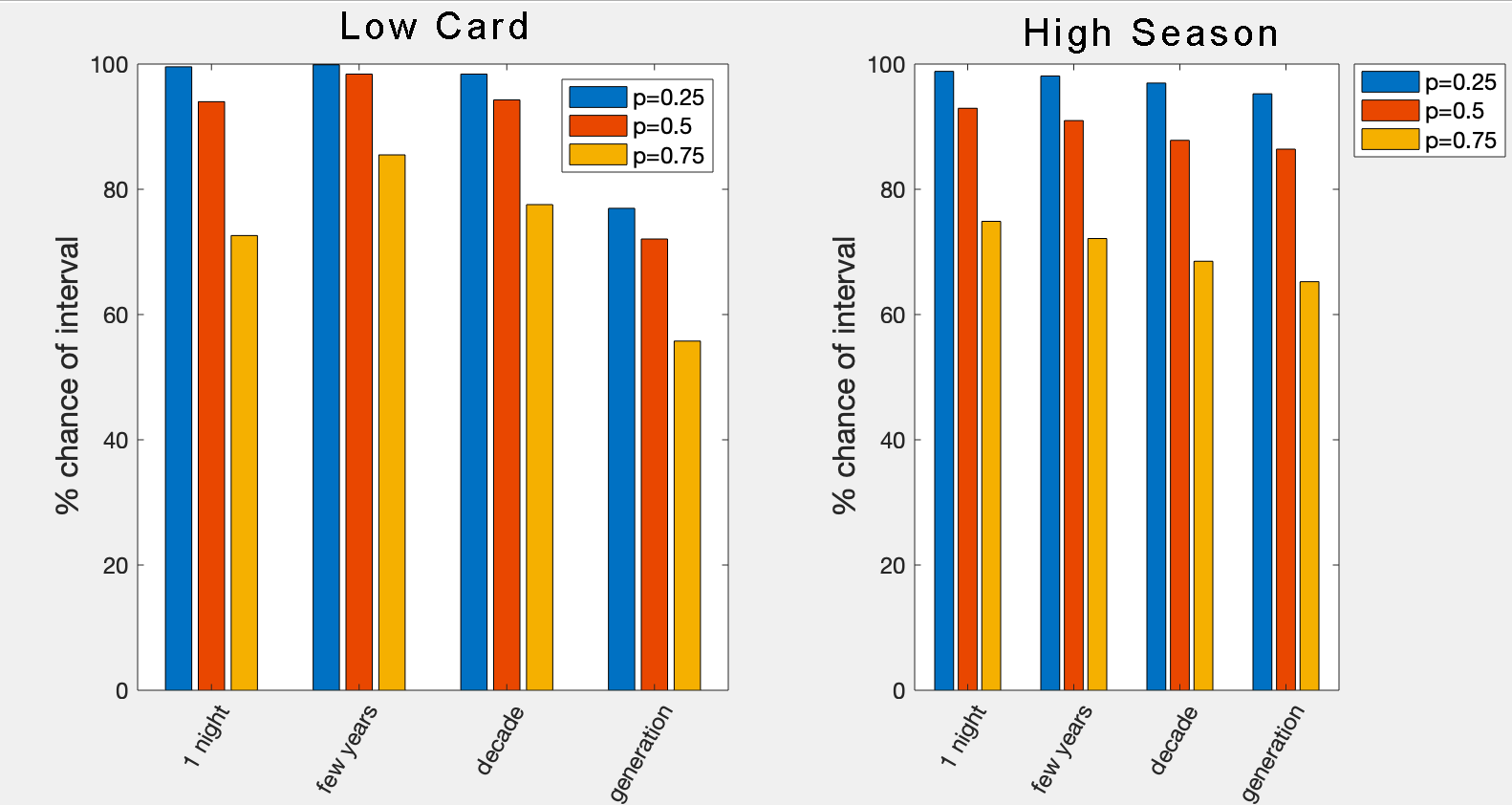
Why am I interested in this? I want most games of TS to include every interval at least once; to be broadly mechanically complete. I want players to have at least one chance to pick something from the 'a generation passes' list on the Interval Oracle. People could always deliberately skew their play to leave low cards on Spring, Summer, and Autumn and enter the interval with a high card on Winter, but I don't want that to be necessary.
What are the results? Bar charts of the % chance that a type of interval will happen at least once per game (e.g. there'll be at least one 'decade' interval).
What does this show? Low Card has a much lower chance of you getting a generation-long Interval than the other types (50-75% for a generation vs 75-100% for the others). High Season is more consistent, even if it's worse overall (especially if you draw more cards per season, which brings all the chances down to 60-80%), and importantly it has a better chance of giving you at least one generation-long Interval.
Q3: how long do games run for (in-game years)?
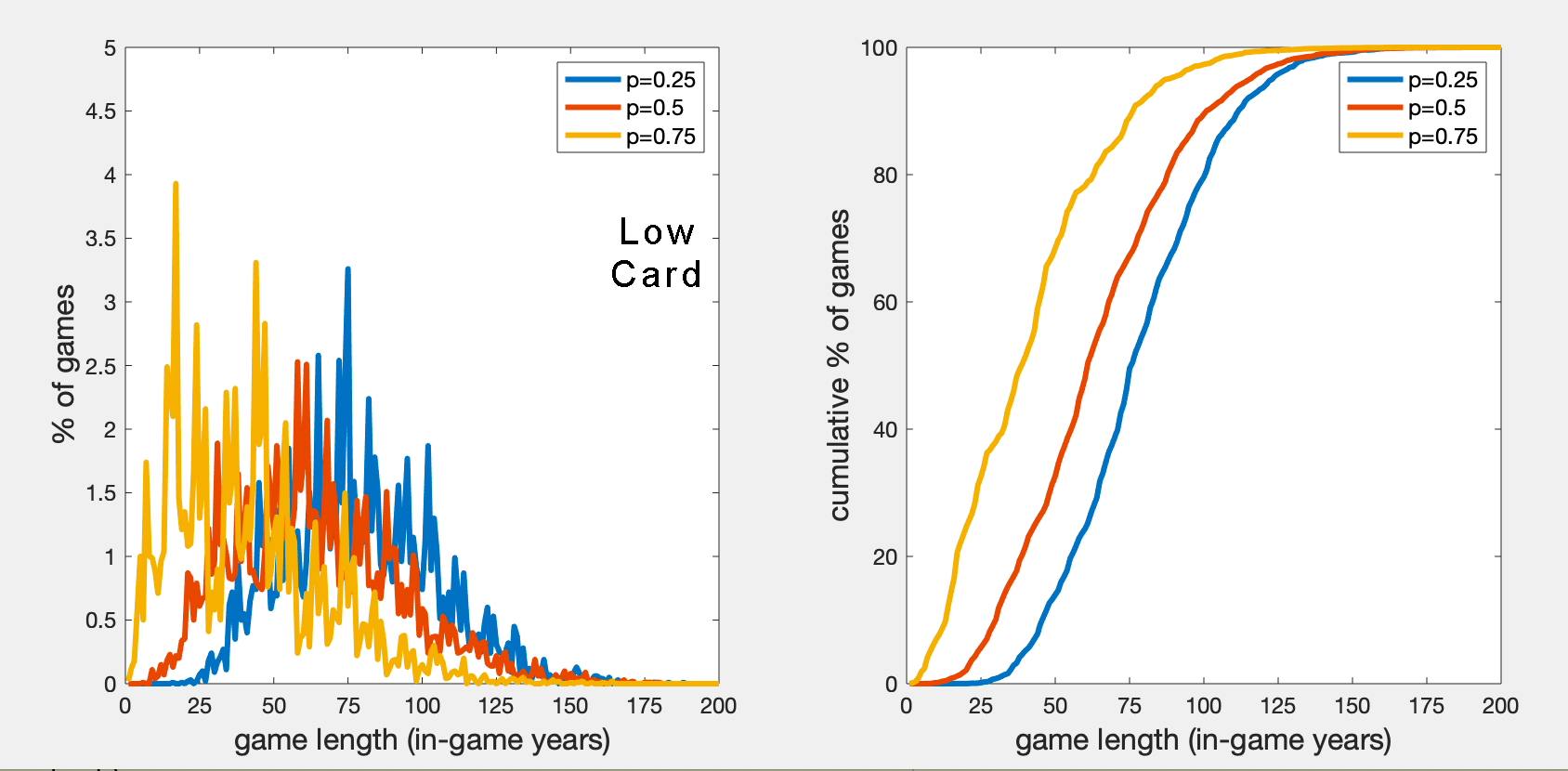
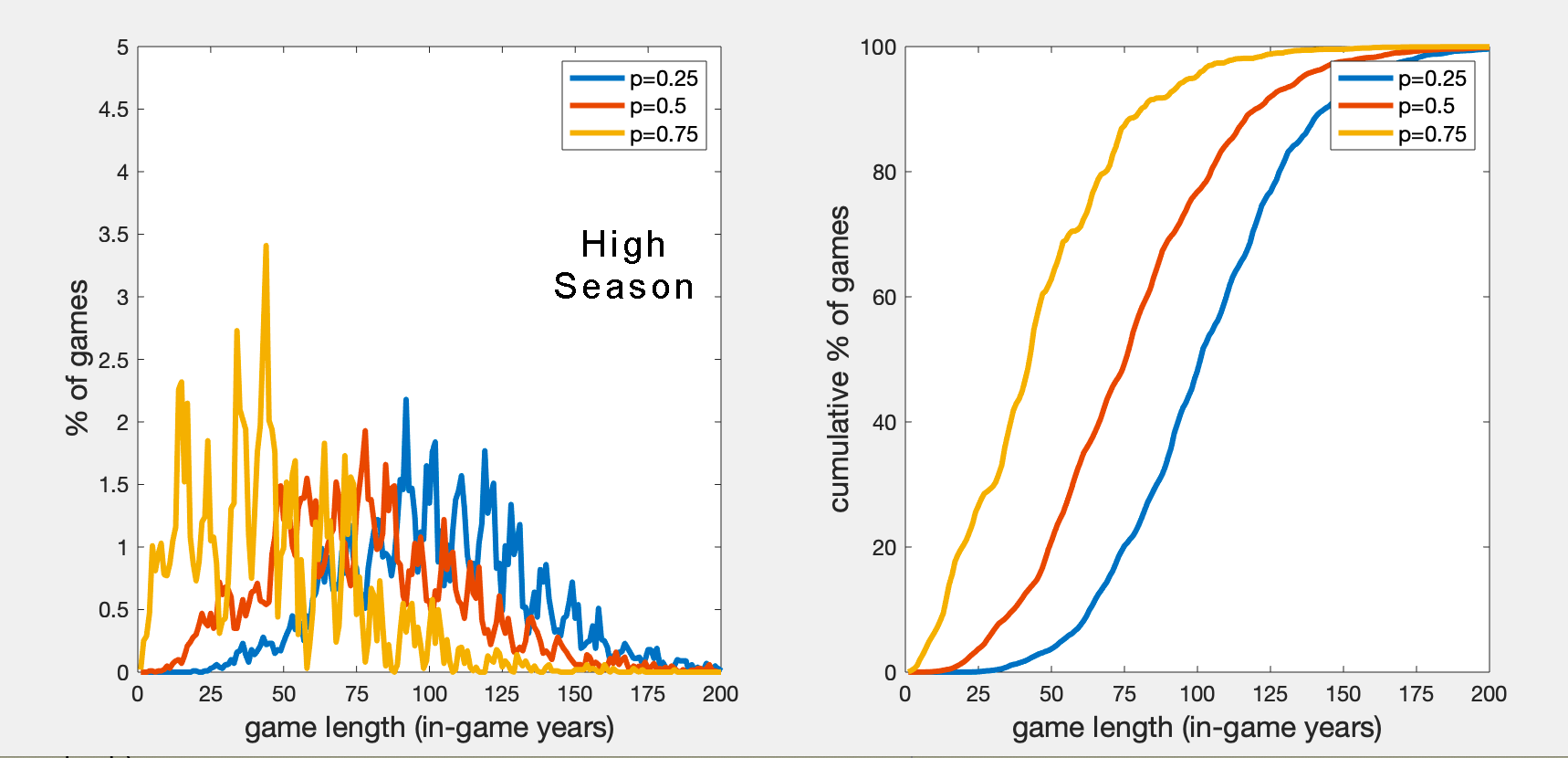
Why am I interested in this? I want the game world and its characters to change dramatically, but at a natural pace. Sometimes big changes can happen quickly, but I want there to be enough time for them to happen slowly and to be experienced as they happen, not just before and after. 50 years is enough for two generations to rise (for people who were young adults at the start to see their grandkids grow up); 100 years is enough for the beginning of your game to pretty much pass from living memory by the end.
What are the results? Regular and cumulative plots of the % of games that run for each number of in-game years.
What does this show? High Season gives better results for me: games cover longer periods, centred on 50-100 years. Also, player choice has more weight (there's a bigger difference between the lines on the cumulative plot). If you want a shorter in-game story, draw more cards in each season.
Bonus: Why are the left-hand curves spiky as fuck? While the interval lengths are kinda vague ('a few years', 'around a decade', 'a generation'), the simulation needed hard numbers. I decided that the intervals were +1 year, +3 years, +10 years, and +30 years. I could set up the simulation to create smoother curves, but it wouldn't tell us anything new. Anyway, this is why I put together the cumulative plots: the slopes on the cumulative plots show where most of the results are on the regular plots, but in a much cleaner way.
What's the verdict?
It's pretty clear: High Season beats Low Card in every aspect (in my opinion, but then, I'm the designer). So, when you read the game, the Interval/Years Between section starts like this:

Low Card isn't bad, just not right for my design goals with TS (I want clear and simple mechanics). I tried tweaking the ranges, but that just makes the mechanic more complicated and less intuitive. High Season does introduce a relationship between oracle prompts and intervals (high Spring/Summer prompts tend to mean short intervals, high Autumn/Winter prompts tend to mean long intervals and vice versa), but the link is pretty weak, so I was willing to accept that as a trade-off.
What does it all mean?
This was a big time-saver! Writing and refining the simulation and doing some data analysis (a chunk of which I haven't posted here) probably took as much time as running a playtest or two, but gave me an insight I'd have needed a lot more tests to get. Sure, I couldn't done a bunch of solo tests where I physically shuffled the decks and drew cards over and over, but 1) that's a bunch of manual labour that doesn't teach me anything and 2) now that I have the code written and tested I can easily make changes and near-instantly get new results. Simulations (and probability calculations) aren't a replacement for playtesting, but they can be a very useful tool alongside them. The maths methods free you up to focus more on the things that you can't simulate or calculate—like how satisfying or enjoyable the game actually is.
I've done the same thing for a bunch of other games of mine where it seemed useful: The Cromlech Archives, Letter Bearer, Dirty Papers, and a slew of unpublished projects. I've also done it with a bunch of games designed by others, including Cthulhu Dark's insanity mechanics, UA's flip-flop dice mechanic, and the now-removed Ross Cowman game Suspended Animation. There'll be more devlogs coming, on itch, twitter (under #rpgmaths), or elsewhere.
If you have any questions about any of this—reasons, methods, results, interpretation—or if you're interested in getting some calculations or simulations done for your own game, let me know.
Files
Get Twilight Song
Twilight Song
what will you do in humanity's twilight?
| Status | Released |
| Category | Physical game |
| Author | Speak the Sky |
| Tags | diceless, GM-Less, journaling, map, One-shot, pastoral, Queer, Sci-fi, tabletop-role-playing-game, world-building |
| Languages | English |
| Accessibility | Color-blind friendly, High-contrast, Blind friendly |
More posts
- Merged with Midnight SignalJul 27, 2024
- Playingcards.io table import!Apr 06, 2021
- Twilight Song v1.1 and Midnight SignalJun 16, 2020

Leave a comment
Log in with itch.io to leave a comment.